DISROPT
Introduction to DISROPT
DISROPT is a Python package for distributed optimization over peer-to-peer networks of computing units called agents.
Objective functions and constraints
DISROPT comes with many already implemented mathematical functions.
Functions are defined in terms of optimization variables (Variable) or other functions. A variable in \(x\in\mathbb{R}^{2}\) can be defined as
from disropt.functions import Variable
n = 2 # dimension of the variable
x = Variable(n)
Now, suppose you want to define an affine function \(f(x)=A^\top x - b\) with \(A\in\mathbb{R}^{2\times 2}\) and \(b\in\mathbb{R}^2\)
import numpy as np
a = 1
A = np.array([[1,2], [2,4]])
b = np.array([[1], [1]])
f = A @ x - b
Constraints are represented in the canonical forms \(f(x)=0\) and \(f(x)\leq 0\).
They are directly obtained from functions::
constraint = g == 0 # g(x) = 0
constraint = g >= 0 # g(x) >= 0
constraint = g <= 0 # g(x) <= 0
On the right side of (in)equalities, numpy arrays and functions (with appropriate shapes) are also allowed::
c = np.random.rand(2,1)
constr = f <= c
which is automatically translated in the corresponding canonical form.
Optimization Problems
The Problem class allows one to define optimization problems of various types. Consider the following problem:
with \(x\in\mathbb{R}^4\). We can define it as
import numpy as np
from disropt.problems import Problem
from disropt.functions import Variable, Norm
x = Variable(4)
A = np.random.randn(n, n)
b = np.random.randn(n, 1)
obj = Norm(A @ x - b)
constr = x >= 0
pb = Problem(objective_function = obj, constraints = constr)
In the distributed framework of DISROPT, the Problem class is mainly meant to define portions of a bigger optimization problem that are locally known to local computing units. However, since in many distributed optimization algorithms can be requested to solve local optimization problems, we implemented some problem solvers. If the problem is convex, it can be solved as
solution = pb.solve()
Generic (convex) nonlinear problems of the form
\[\begin{align} \text{minimize } & f(x) \\ \text{subject to } & g(x) \leq 0 \\ & h(x) = 0 \end{align}\]are solved through the cvxpy solver (when possible), or with the cvxopt solver, while more structured problems (LPs and QPs) can be solved through other solvers (osqp and glpk). Mixed-Integer Problems can be solved using gurobi.
Agents in the network
The Agent class is meant to represent the local computing units that collaborate in the network in order to solve some specific problem.
Agents are instantiated by defining their in/out-neighbors and the weights they assign their neighbors. For example, consider the following network
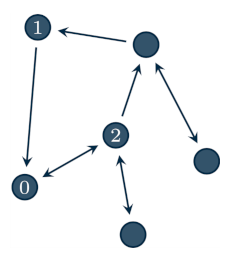
Then, agent 0 is defined as
from disropt.agents import Agent
agent = Agent(in_neighbors=[1,2],
out_neighbors=[2],
weights=[0.3, 0.2])
Assigning a local optimization problem to an agent is done via the set_problem method, which modifies the problem attribute of the agent. Consider the following code
from disropt.problems import Problem
from disropt.functions import Variable, Norm
x = Variable(4)
A = np.random.randn(n, n)
b = np.random.randn(n, 1)
obj = Norm(A @ x - b)
constr = x >= 0
pb = Problem(objective_function = obj, constraints = constr)
Assume that the variable problem contains the local problem data. Then, the variable is assigned to the agent by
agent.set_problems(problem)
Distributed Optimization Algorithms
In DISROPT, there are many implemented distributed optimization algorithms. Each algorithm is tailored for a specific distributed optimization set-up. We refer the reader to the DISROPT documentation page for a detailed explanation.
Planning of Battery Charging for Electric Robots in DISROPT
In the following, we consider a charging scheduling problem in a fleet of \(N\) battery-operated robots drawing power from a common infrastructure. We refer the reader to the paper for additional details.
Problem formulation
The considered schedule has to satisfy local requirements for each robot, e.g., the final state of charge (SoC). The schedule also has to satisfy power constraints, e.g., limits on the maximum power flow. We assume that charging can be interrupted and resumed. The overall charging period \(T\) is discretized into \(d\) time steps. For each robot \(i \in \{1,\ldots,N\}\), let \(u_i\in[0,1]^d\) be a set of decision variables handling the charging of the robot. That is robot \(i\) charges at time step \(k\) with a certain charge rate between \(0\) (no charging) and \(1\). The \(i\)-th battery charge level during time is denoted by \(e_i\in\mathbb{R}^d\). The \(i\)-th battery initial SoC is \(E_i^\text{init}\) and, at the end of the charging period, its SoC must be at least \(E_i^\text{ref}\). We denote by \(E_i^\text{min}\) and \(E_i^\text{max}\) the battery’s capacity limits, by \(P_i\) the maximum charging power that can be fed to the \(i\)-th robot, and by \(P^{\text{max}}\) the maximum power flow that robots can draw from the infrastructure. Let \(C_u^k\in\mathbb{R}\) be the price for electricity consumption at time slot \(k\). Let \(\mathbb{T}\) denote the set \(\{0,\dots,T-1\}\). The objective is to minimize the cost consumption. Then, the optimization problem can be cast as
\[\begin{align} \underset{\{e_i,u_i\}_{i=1}^N}{\text{min}} & \sum\limits_{i=1}^N \sum_{k=0}^{T-1} P_i C_u^k u_i^k \\ \text{subj. to } & \sum\limits_{i=1}^N P_iu_i^k \leq P^{\text{max}} & \forall k\in\mathbb{T} \\ & e_i^0 = E_i^\text{init} & \forall i\in\{1,\ldots,N\} \\ & e_i^{k+1}= e_i^k +\!P_i \Delta T u_i^k & \forall i\in\{1,\ldots,N\}, k\in\mathbb{T} \\ & e_i^T \geq E_i^\text{ref} & \forall i\in\{1,\ldots,N\} \\ & E_i^\text{min}1_d \leq e_i \leq E_i^\text{max}1_d & \forall i\in\{1,\ldots,N\} \\ & u_i \in [0,1]^d & \forall i\in\{1,\ldots,N\}. \end{align}\]Implementation of the optimization problem
We refer the reader to the tutorial paper for details on the data generation model.
import numpy as np
from numpy.random import uniform as rnd
from mpi4py import MPI
from disropt.agents import Agent
from disropt.functions import Variable
from disropt.problems import ConstraintCoupledProblem
# get MPI info
NN = MPI.COMM_WORLD.Get_size()
agent_id = MPI.COMM_WORLD.Get_rank()
#### Common parameters
TT = 24 # number of time windows
DeltaT = 20 # minutes
PP_max = 0.5 * NN # kWh
CC_u = rnd(19,35, (TT, 1)) # EUR/MWh - TT entries
np.random.seed(10*agent_id)
PP = rnd(3,5) # kW
EE_min = 1 # kWh
EE_max = rnd(8,16) # kWh
EE_init = rnd(0.2,0.5) * EE_max # kWh
EE_ref = rnd(0.55,0.8) * EE_max # kWh
zeta_u = 1 - rnd(0.015, 0.075) # pure number
# normalize unit measures
DeltaT = DeltaT/60 # minutes -> hours
CC_u = CC_u/1e3 # Euro/MWh -> Euro/KWh
# optimization variables
z = Variable(2*TT + 1) # stack of e (state of charge) and u (input charging power)
e = np.vstack((np.eye(TT+1), np.zeros((TT, TT+1)))) @ z # T+1 components (from 0 to T)
u = np.vstack((np.zeros((TT+1, TT)), np.eye(TT))) @ z # T components (from 0 to T-1)
# objective function
obj_func = PP * (CC_u @ u)
# coupling function
coupling_func = PP*u - (PP_max/NN)
# local constraints
e_0 = np.zeros((TT+1, 1))
e_T = np.zeros((TT+1, 1))
e_0[0] = 1
e_T[TT] = 1
constr = [e_0 @ e == EE_init, e_T @ e >= EE_ref] # feedback and reference constraints
for kk in range(0, TT):
e_cur = np.zeros((TT+1, 1))
u_cur = np.zeros((TT, 1))
e_new = np.zeros((TT+1, 1))
e_cur[kk] = 1
u_cur[kk] = 1
e_new[kk+1] = 1
constr.append(e_new @ e == e_cur @ e + PP*DeltaT*zeta_u*u_cur @ u) # dynamics
constr.extend([u_cur @ u <= 1, u_cur @ u >= 0]) # input constraints
constr.extend([e_new @ e <= EE_max, e_new @ e >= EE_min]) # state constraints
pb = ConstraintCoupledProblem(obj_func, constr, coupling_func)
Implementation of graph-related data and network agent
from disropt.agents import Agent
from disropt.utils.graph_constructor import binomial_random_graph, metropolis_hastings, binomial_random_graph_sequence
# Generate a common graph (everyone uses the same seed)
Adj = binomial_random_graph(NN, p=0.2, seed=1)
W = metropolis_hastings(Adj)
# local agent and problem
agent = Agent(
in_neighbors=np.nonzero(Adj[agent_id, :])[0].tolist(),
out_neighbors=np.nonzero(Adj[:, agent_id])[0].tolist(),
in_weights=W[agent_id, :].tolist())
pb = ConstraintCoupledProblem(obj_func, constr, coupling_func)
agent.set_problem(pb)
Instantiate distributed optimization algorithms
from disropt.algorithms import PrimalDecomposition
from dualdecomposition import DualDecomposition
# instantiate the algorithms
y0 = 10*np.random.rand(TT, 1)
mu0 = 10*np.random.rand(TT, 1)
theothers = [i for i in range(NN) if i != agent_id]
y_others = agent.communicator.neighbors_exchange(y0, theothers, theothers, False)
y_others[agent_id] = y0
y_mean = sum([x for _, x in y_others.items()])/NN
y0 -= y_mean
dds = DualDecomposition(agent=agent,
initial_condition=mu0,
enable_log=True)
dpd = PrimalDecomposition (agent=agent,
initial_condition=y0,
enable_log=True)
num_iterations = 1000
# define a stepsize generator
def step_gen(k):
return 1/((k+1)**0.6)
# run the algorithms
if agent_id == 0:
print("Distributed dual subgradient")
_, dds_seq = dds.run(iterations=num_iterations, stepsize=step_gen, verbose=True)
if agent_id == 0:
print("Distributed primal decomposition")
dpd_seq, _, _ = dpd.run(iterations=num_iterations, stepsize=step_gen, M=30.0, verbose=True)
Save the data
# save information
if agent_id == 0:
with open('info.pkl', 'wb') as output:
pickle.dump({'N': NN, 'iterations': num_iterations, 'n_coupling': TT}, output, pickle.HIGHEST_PROTOCOL)
with open('agent_{}_objective_func.pkl'.format(agent_id), 'wb') as output:
pickle.dump(obj_func, output, pickle.HIGHEST_PROTOCOL)
with open('agent_{}_coupling_func.pkl'.format(agent_id), 'wb') as output:
pickle.dump(coupling_func, output, pickle.HIGHEST_PROTOCOL)
with open('agent_{}_local_constr.pkl'.format(agent_id), 'wb') as output:
pickle.dump(constr, output, pickle.HIGHEST_PROTOCOL)
np.save("agent_{}_seq_dds.npy".format(agent_id), dds_seq)
np.save("agent_{}_seq_dpd.npy".format(agent_id), dpd_seq)
Run the example
We refer the reader to the git page for the complete code and for information on how to install DISROPT.
In oder to launch the distributed optimization with \(N=50\) robots, it is sufficient to run
mpirun -np 50 --oversubscribe python launcher.py
To plot the results instead
python results.py