ChoiRbot
Introduction to ChoiRbot
ChoiRbot is a is a ROS 2 package to simulate and run experiments on teams of cooperating robots.
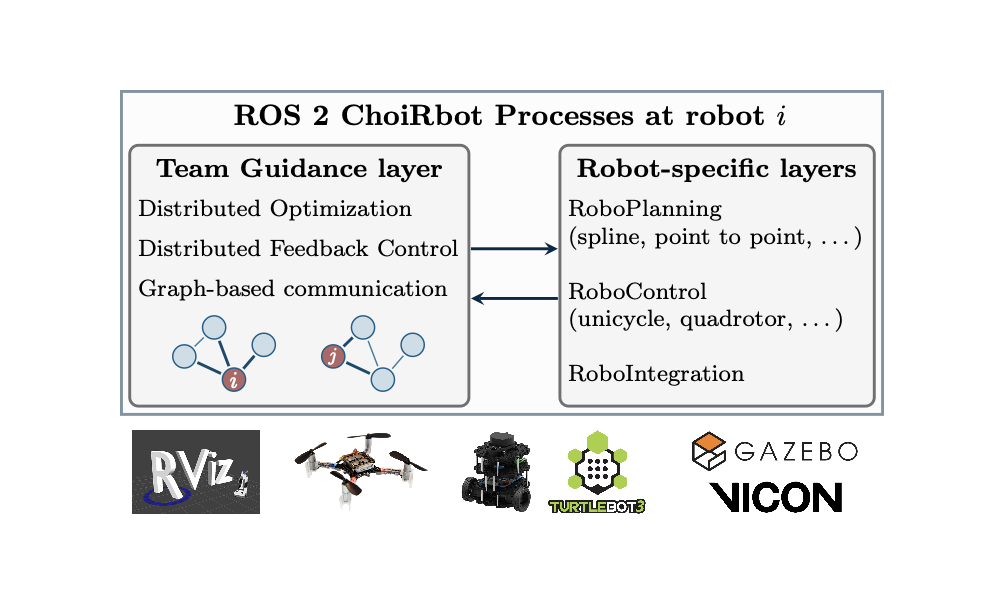
Three-Layer architecture of ChoiRbot
ChoiRbot employs a three-layer architecture made of the Team Guidance, RoboPlanning, and RoboControl layers. The Team Guidance layer oversees high-level decision-making and robot lifecycle management, utilizing communication with neighboring entities for task execution. To this end, it is compatible with DISROPT. The RoboPlanning and RoboControl layers handle lower-level control actions and receive setpoints from the guidance layer. Additionally, a dynamics integration layer called RoboIntegration is provided. This layer facilitates integration, such as with RViz for visualization purposes.
Simulate a Robot
In ChoiRbot, robots can be simulated in two different ways. The first one is to leverage an external tool such as, e.g., Gazebo. The second one is to extend the Integrator class of the RobotIntegration layer. We will focus on this second point.
Suppose that we are interested into simulating a robot subject to single-integrator dynamics in the form
where \(x\in\mathbb{R}^{3}\) is the 3D position of the robot while \(u\in\mathbb{R}^{3}\) is a suitable control input. In the Integrator class, the position of the robot is stored in a variable called current_pos. The update of the dynamics is instead defined into an integrate() method. Thus, we have to specify how to update current_pos. Finally, we have to specify how to receive a control input. To this end, we have to define a ROS 2 subscription. A possible example for this class follows.
from choirbot.integrator import Integrator
from geometry_msgs.msg import Vector3
import numpy as np
class SingleIntegrator(Integrator):
def __init__(self, integration_freq: float, odom_freq: float=None):
super().__init__(integration_freq, odom_freq)
# create input subscription
self.u = np.zeros(3)
self.subscription = self.create_subscription(Vector3, 'velocity', self.input_callback, 1)
self.get_logger().info('Integrator {} started'.format(self.agent_id))
def input_callback(self, msg):
# save new input
self.u = np.array([msg.x, msg.y, msg.z])
def integrate(self):
self.current_pos += self.samp_time * self.u
Here, we update the position using the Euler update. We receive inputs from a velocity topic. This class will publish an Odometry message into an odom topic. All the machinery is already enclosed into the Integrator class.
Notice that the class has a field named agent_id. This represents a unique numerical identifier for the robot and allows to instantiate a network of cooperating robots. This field also ensure uniqueness on the topic names by creating suitable namespaces for each robot. As an example, if agent_id=0, the robot will communicate on topic /agent_0/odom and /agent_0/velocity.
Implement a Control Law
Suppose now that we want to implement a proportional control law for the single-integrator system, i.e.
\[\begin{align} u(t) = K*(x(t)-x_d), \end{align}\]for a given goal \(x_d\) and a suitable \(K\). To do this, we can extend the Controller class of ChoiRbot as follows.
from choirbot.controller import Controller
from geometry_msgs.msg import Vector3, Point
import numpy as np
class ProportionalController(Controller):
def __init__(self, pos_handler: str=None, pos_topic: str=None):
super().__init__(pos_handler, pos_topic)
self.pub= self.create_publisher(Vector3, 'velocity')
self.timer = self.create_timer(0.05, self.control_callback)
self.goal = None
self.goal_sub = self.create_subscription(Point,'goal', self.goal_callback, 1)
self.get_logger().info('Controller {} started'.format(self.agent_id))
def control_callback(self):
# skip if position or goal is not available yet
if self.current_pose.position is None or self.goal is None:
return
pos = self.current_pose.position
k = -0.3
v=k*np.array([pos-self.goal[0], pos-self.goal[1], pos-self.goal[2]])
self.send_input(v)
def send_input(self, v):
msg = Vector3(v[0], v[1], v[2])
self.pub.publish(msg)
def goal_callback(self, msg):
self.goal = [msg.x, msg.y, msg.z]
self.get_logger().info('Received goal {}'.format(self.goal))
The Controller class already handles how to receive odometry data from the integrator or an external simulation tool. Thus, we only need to create a publisher to send input data. To this end, we created a velocity topic. Notice that this name matches the one in the integrator class. The goal point will be received instead on a suitable goal topic.
Interfacing with Gazebo
ChoiRbot can be interfaced with external tools to leverage realistic simulations. In the turtlebot_spawner.py we provide a class that enables to spawn an arbitrary number of Turtlebot3 mobile robots in a certain position with a given namespace. To this end, we use a dedicated node interfacing with the SpawnEntity service provided by the Gazebo ros factory plugin. It is implemented in the file turtlebot_spawner.py in the
choirbot_examples package.
This service requires the Gazebo process to be executed with the following command
gazebo -s libgazebo_ros_factory.so
After each robot is created (suppose with the namespace agent_0), Gazebo will publish
its updated pose in the /agent_0/odom topic, which is retrieved by the Team guidance
class to compute the control input. Robots receive commands in the /agent_0/cmd_vel
topic as published by the unicycle control.
Multi-Robot Multi-Task Assignment in ChoiRbot
In the following, we consider a task assignment scenario in which a team of \(N\) robots has to self-assign a set of \(N\) tasks. We refer the reader to the paper for additional details.
Problem formulation
We consider a team of robots that must self-assign a set of tasks while minimizing the total robot path length. Assume there are \(N\) robots (indexed by \(i\)) and \(N\) tasks (indexed by \(k\)). A scalar \(c_{ik}\) represents the cost incurred by robot \(i\) when servicing task \(k\). The goal is to find the optimal assignment, i.e. to assign each robot \(i\) to exactly one task \(j\) such that the total incurred cost is minimized. To compute the optimal assignment, robots must solve the following linear program
\[\begin{aligned} \min_{x} \: & \: \sum_{i, k} c_{ik} x_{ik} \\ \text{subj. to} \: & \: 0 \leq x_{ij} \leq 1, \hspace{0.5cm} \forall \: i, k \\ & \: \sum_{k} x_{ik} = 1 \hspace{0.5cm} \forall \: i, \\ & \: \sum_{i} x_{ik} = 1 \hspace{0.5cm} \forall \: k. \end{aligned}\]Implementation in ChoiRbot
In order to implement the dynamic task assignment example in ChoiRbot, we consider the following nodes for each robot:
- a Team Guidance node that receives task requests, runs the distributed optimization algorithm (which requires communication with the neighbors) to determine the task assigned to the robot and triggers execution of the task to the planning node
- a Planning node that receives the target positions and interfaces with the Control node to reach those positions
- a Control node implementing a closed-loop unicycle controller to reach the designated positions
For this simulation we also consider an additional “Task table” node that generates the tasks requests and sends them to the robots.
To run the simulation, we will also need to interface ChoiRbot with Turtlebot3 robots in Gazebo. Finally, we will also need a launch file and the executable scripts (as required by the ChoiRbot paradigm).
Task table
The task table is implemented in the class choirbot.guidance.task.PositionTaskTable and is
responsible for maintaining the list of task requests. The flow of the class is as follows
- initially, the class generates \(N\) task requests;
- the class sends a trigger signal to the robots to inform that the task list has changed;
- each robot can retrieve the updated task list from the table by using a ROS service;
- robots run the optimization algorithm to compute the assignment and moves towards the task;
- as soon as robot \(i\) reaches task \(j\) it stands still on it for some seconds to simulate the execution of a task. Also, robot \(i\) informs the class that task \(j\) has been executed by using a ROS service;
- the class generates a new task and repeats step 2.
Moreover
- each task is characterized by a sequence number (
seq_num) and an ID (id). Theseq_numis unique and is different for each task generated by the class throughout its execution, while IDs always belong to the range \(\{0, \ldots, N-1\}\) such that each task processed within the same optimization problem have different IDs, thus they are re-used throughout the execution of the class (recall that in each optimization problem solved by the robots there are always exactly \(N\) tasks); - the list received by each robot \(i\) contains only the tasks that can be potentially performed by robot \(i\). Other tasks are disallowed and can only be performed by other robots.
Team guidance
The team guidance layer of each robot is implemented in the class
choirbot.guidance.task.TaskGuidance and is responsible for the execution of
tasks (by interacting with the local planning layer), the execution of the distributed
optimization algorithm and for interfacing with the task table.
The flow of the class is as follows
- when the class receives the trigger signal from the task table, it asks for the updated
task list and waits for it on the separate optimization thread implemented with the
class
choirbot.guidance.task.task.TaskOptimizationThread; - upon receiving the new task list, the optimization thread starts the distributed optimization algorithm, which will require communication with neighbors;
- when the optimization is completed, the main thread saves the queue of tasks to be executed by the robot (in this example each robot is assigned exactly one task so the queue contains only one task). If a task is currently being executed by the class, it is canceled;
- the class executes the enqueued tasks in order until the queue is empty;
- if a new trigger signal is received from the task table, the task queue is emptied and the class keeps on executing the task that is currently in progress. Meanwhile, step 1 is repeated.
Solving the optimization problem requires an Optimizer class. In this example, this is implemented with a suitable class that which formulates the task assignment problem and executes the Distributed Dual Decomposition algorithm.
Planning
The planning node is implemented in the choirbot.planner.TwoDimPointToPointPlanner class.
It simply consists of a ROS action that receives target positions from the Team guidance layer
and forwards them to the control node on a goal ROS topic. Tasks currently in execution are aborted
if the Team guidance layer sends a new action request prematurely.
Running the simulation
To run the simulation, we simply need to execute the launch file. First we source the workspace:
source install/setup.bash
Now we are ready to run the example:
ros2 launch choirbot_examples taskassignment.launch.py
A Gazebo window will open. After a few seconds, the task table generates tasks and robots start to move to their target positions: